Wie berechnet man THD und PF?

Wie berechnet man THD und PF?

 

Analyse der gesamten harmonischen Verzerrung (THD) und Bewertung des Leistungsfaktors. In dieser Diskussion untersuchen wir Methoden zur Messung der gesamten harmonischen Verzerrung sowie Berechnungen für den Leistungsfaktor.

Die Gesamtverzerrung (THD) ist ein Maß, das die Summe der harmonischen Frequenzen widerspiegelt, die der Primärfrequenz (z. B. 60 Hz) in einem Stromkreis gegenübergestellt werden. Sie umfasst alle vorhandenen harmonischen Frequenzen. Die Gesamtverzerrung kann mit Strom- oder Spannungsoberwellen in Zusammenhang stehen. Um die Verzerrung der Netzspannung zu quantifizieren, wenden Sie die folgende Formel an:

 

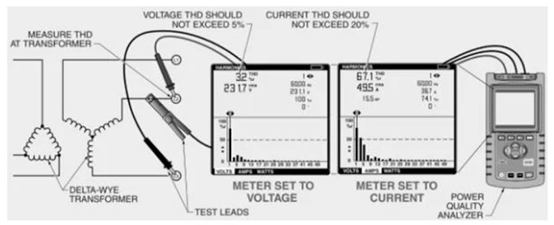
Abbildung 1. Die THD-Messung sollte am Transformator und nicht in der Nähe der Last durchgeführt werden.

Dabei ist Vn_rms die Effektivspannung der n-ten Harmonischen und Vfund_rms die Effektivspannung der Grundfrequenz. Eine reine Sinuswelle ohne höhere Harmonische, wie eine einwandfreie Spannungsquelle, weist einen THD von 0 % auf. Jeder THD-Wert über Null weist auf eine Verzerrung der Sinuswelle hin. THD-Werte werden normalerweise als Prozentwerte angegeben, z. B. 5 % oder 50 %. THD kann sowohl für Strom- als auch für Spannungssignale ermittelt werden.

Harmonische Ströme entstehen durch nichtlineare Lasten, die Strom in Impulsen ziehen. Spannungsoberwellen entstehen durch diese Ströme, die durch verschiedene Systemwiderstände fließen. Transformatorstrom verursacht einen Spannungsabfall über seinen Spulen. Wenn der Strom pulsiert, spiegelt die Spannung diese Pulsation wider. Übermäßige Spannungsverzerrungen sind schädlich, da sie als Kanal für Harmonische zu linearen Lasten wie Elektromotoren dienen. Spannungsoberwellen führen zu zusätzlicher Erwärmung in Stromverteilungssystemen und angeschlossenen Geräten.

 

Messen des Klirrfaktors

Bei der Fehlersuche in Schaltkreisen auf Oberschwingungen müssen Sie sowohl den Spannungs-THD als auch den Strom-THD messen. Ideale Ergebnisse sind, wenn der Spannungs-THD 5 % nicht überschreitet und der Strom-THD unter 20 % der Grundfrequenz bleibt. Der THD sollte auf Transformatorebene ausgewertet werden, um eine genaue systemweite THD-Berechnung zu ermöglichen (siehe Abbildung 1). Lastseitige THD-Messwerte bieten die höchsten Werte, da im gesamten System keine Oberschwingungsauslöschung aufgetreten ist.

 

Bei der Messung des THD-Stroms unter Volllastbedingungen ist der THD mit der Gesamtlastverzerrung (TDD) vergleichbar. TDD ist der Quotient aus Stromoberwellen und dem maximalen Laststrom. Eine THD-Messung wird bei der Diagnose oder Prüfung von Systemen durchgeführt. TDD unterscheidet sich vom THD, da TDD mit der Messung des Spitzenstroms über einen bestimmten Zeitraum verglichen wird. THD misst ausschließlich den Strom zum Zeitpunkt der Messung. Die Rolle von TDD besteht darin, Fälle zu berücksichtigen, in denen der THD erhöht ist, die Gesamtlast jedoch relativ gering ist. Unter solchen Umständen ist TDD moderat und minimiert Überhitzung.

 

Leistungsfaktor

 

Power factor delineates the ratio of authentic power to apparent power in a circuit or distribution network. Every AC circuit is comprised of real, reactive, harmonic, and apparent (aggregate) power. True power, in watts or kilowatts, is expended by motors, lighting, and other apparatuses to execute functional tasks. Reactive power, in volt-amperes reactive or kilovolt-amperes reactive, is stored and discharged by inductors and capacitors. Reactive power materializes as phase displacement between current and voltage waveforms. Harmonic power, in volt-amperes or kilovolt-amperes, is dissipated due to harmonic distortion. Apparent power, in volt-amperes or kilovolt-amperes, is the vectorial sum of true power, reactive power, and harmonic power. Apparent power isn't a simple accumulation but a vector summation.

 

Displacement Power Factor

 

The displacement power factor is the ratio of genuine power to apparent power attributable to phase displacement between current and voltage (as shown in Illustration 2). Capacitors can frequently be integrated into a circuit or distribution network to rectify the displacement power factor. Its computation is as follows:

PF = cos(θ)

where PF signifies displacement power factor and θ is the discrepancy between voltage and current phases in degrees. Note: DPF or PFD may occasionally substitute PF to denote displacement power factor.

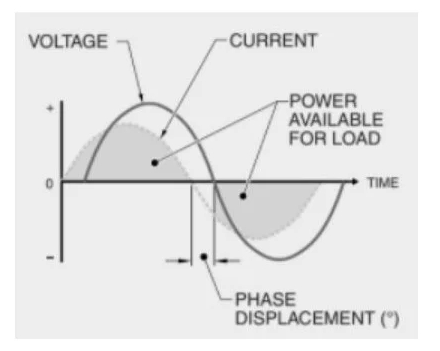
Figure 2. Displacement power factor enables calculation of the power genuinely accessible for a load.

 

 

The presence of harmonics introduces complexity into the discussion of power factor. The distortion power factor, defined as the ratio of true power to apparent power due to Total Harmonic Distortion (THD), cannot be mitigated simply by adding capacitors to a circuit. This is because the impedance of capacitors decreases with an increase in frequency, potentially turning them into sinks for high-frequency harmonics rather than effective compensators.

 

To address the distortion power factor, specialized solutions are employed. These include special types of transformers designed to handle harmonic loads or tuned harmonic filters that consist of a combination of capacitors and inductors. Such filters are specifically engineered to resonate at harmonic frequencies, effectively absorbing or cancelling out these distortions.

 

The calculation of the distortion power factor involves assessing the impact of harmonic content on the overall power factor, reflecting the diminished efficiency caused by the presence of these higher-order frequencies in the electrical system.

The distortion power factor is calculated as follows:

.

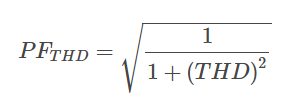
where
PFTHD = distortion power factor
THD = total harmonic distortion

The total power factor is the product of the displacement power factor and the distortion power factor and is calculated as follows:

PFTot = PF × PFTHD

where
PFTot = total power factor
PF = displacement power factor
PFTHD = distortion power factor

For example, what is the total power factor when the displacement between voltage and current is 25°, and the THD is 49% (0.49)? The displacement power factor is calculated as follows:

PF = cos(θ)
PF = cos (25°)
PF = 0.906

The distortion power factor is calculated as follows:

.

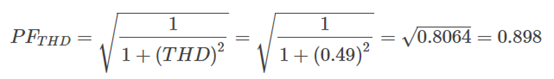The total power factor is calculated as follows:

PFTot = PF × PFTHD
PFTot = 0.906 × 0.898
PFTot = 0.814

Understanding the total power factor is crucial as it directly correlates with apparent power, which is fundamental in sizing components within a power distribution system. Apparent power serves as a key metric for ensuring that all elements in the system are appropriately rated to handle the electrical load without being overloaded.

 

Current Crest Factor

 

The current crest factor, defined as the ratio of the waveform's peak value to its RMS value, serves to indicate the extent of distortion in the waveform. Its calculation provides insights into the waveform's quality, with higher factors pointing to greater levels of distortion. The formula for determining the current crest factor is as follows:

.

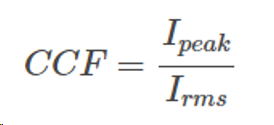where
CCF = current crest factor
Ipeak = peak value (in A)
Irms = root mean square value (in A)

For example, what is the current crest value of a perfect sine waveform? In a perfect sine waveform with a peak value of 1, the rms value is 0.707.

.

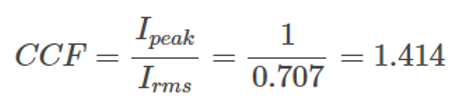An elevated current crest factor can result in excessive heat generation within circuits and devices. For instance, on a 120V circuit powering digital equipment such as computers, a distorted current waveform might display a crest factor ranging from 2 to 6 (consult Figure 3). Typically, circuits with a higher current crest factor contain a greater proportion of energy in their higher harmonics.

 

A power source is obligated to provide the peak power needed by the circuit, matching the specified voltage and current demands. A conventional backup power system, such as an uninterruptible power supply for computers, is capable of delivering a current crest factor of 3 when operating at full capacity but may experience augmented crest factors under lighter load conditions.

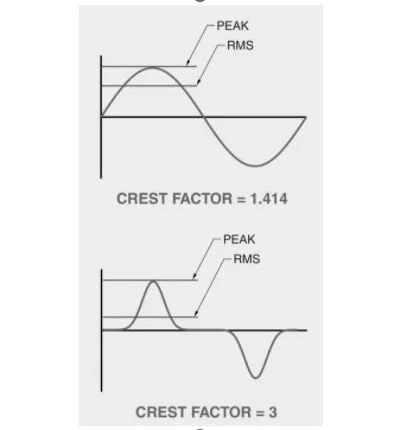
Figure 3. The current crest factor comparison

 

 Source Impedance

 

Die Quellenimpedanz beeinflusst den Scheitelfaktor, der durch nichtlineare Lasten erzeugt wird. Beim Erreichen einer bestimmten Spannungsschwelle leitet die Stromversorgung das Laden eines Glättungskondensators ein. Wenn die Quellenimpedanz minimal ist, ist der Stromstoß in den Kondensator beträchtlich, was zu einer kurzen Ladedauer führt. Umgekehrt begrenzt eine höhere Impedanz den Stromfluss und verlängert dadurch die Ladezeit des Kondensators. Dieses verlängerte Ladeintervall verringert effektiv den Scheitelfaktor. Man kann die Quellenimpedanz durch den Einbau von Netzdrosseln oder Antriebsisolationstransformatoren erhöhen.